If the right string is a ``brick wall" then (i.e.
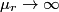 ) then the transmitted amplitude is 0. If the right string is identical to the left string (i.e. ) then the transmitted amplitude is 0. If the right string is identical to the left string (i.e. 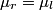 ) then the transmitted amplitude is 0. Both situations are possible, so in fact answers (A) and (E) are both wrong. ) then the transmitted amplitude is 0. Both situations are possible, so in fact answers (A) and (E) are both wrong.Now, consider the case where 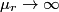 again. In this limit, answers (B) and (D) give 2 and -1 respectively. Therefore, these answers must both be wrong. This eliminates all answers except answer (C), therefore answer (C) is the correct one. And indeed, answer (C) goes to 0 as again. In this limit, answers (B) and (D) give 2 and -1 respectively. Therefore, these answers must both be wrong. This eliminates all answers except answer (C), therefore answer (C) is the correct one. And indeed, answer (C) goes to 0 as 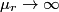 . .\section*{alternative solution:} Let 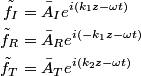 be the incident, reflected, and transmitted waves respectively. Actually, the real parts of these functions are the incident, reflected, and transmitted waves respectively. The wave must be continuous at 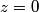 . Also, the derivative of the wave must be continuous at . Also, the derivative of the wave must be continuous at 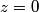 because the problem statement does not gives us the mass of the knot. Therefore, because the problem statement does not gives us the mass of the knot. Therefore,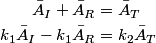 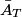 can be easily found from these equations: can be easily found from these equations: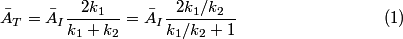 Recall the following relationships: 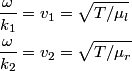 These imply that 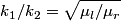 Plugging this into equation 1 gives  Presumably, the amplitudes referred to in the problem statement are the real amplitudes 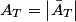 and and 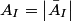 . By taking the modulus of both sides of equation 2, we find that . By taking the modulus of both sides of equation 2, we find that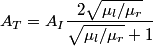 We are given that 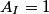 . Therefore, . Therefore, 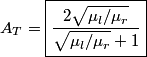 Therefore, answer (C) is correct. |